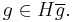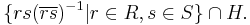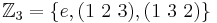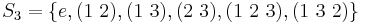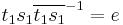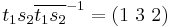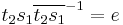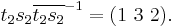Schreier's subgroup lemma
Schreier's subgroup lemma is a theorem in group theory used in the Schreier–Sims algorithm and also for finding a presentation of a subgroup.
Definition
Suppose  is a subgroup of
is a subgroup of  , which is finitely generated with generating set
, which is finitely generated with generating set  , that is, G = <S>.
, that is, G = <S>.
Let  be a right transversal of
be a right transversal of  in
in  .
.
We make the definition that given  ∈
∈ ,
, 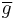 is the chosen representative in the transversal
is the chosen representative in the transversal  of the coset
of the coset 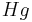 , that is,
, that is,
Then  is generated by the set
is generated by the set
Example
Let us establish the evident fact that the group Z3=Z/3Z is indeed cyclic. Via Cayley's theorem, Z3 is a subgroup of the symmetric group S3. Now,
where  is the identity permutation. Note S3 = < { s1=(1 2), s2=(1 2 3) } >.
is the identity permutation. Note S3 = < { s1=(1 2), s2=(1 2 3) } >.
Z3 has just two cosets, Z3 and S3 \ Z3, so we select the transversal { t1=e, t2=(1 2) }, and we have
Finally,
Thus, by Schreier's subgroup lemma, { e, (1 3 2) } generates Z3, but having the identity in the generating set is redundant, so we can remove it to obtain another generating set for Z3, { (1 3 2) } (as expected).
References
- Seress, A. Permutation Group Algorithms. Cambridge University Press, 2002.